Задание 1 ЕГЭ по профильной математике

В данном задании требуется решить планиметрическую задачу по геометрии.

По спецификации ЕГЭ в задаче проверяются умение решать планиметрические задачи на нахождение геометрических величин (длин, углов, площадей); способность моделировать реальные ситуации на языке геометрии; исследовать построенные модели с использованием геометрических понятий и теорем, аппарата алгебры; решать практические задачи, связанные с нахождением геометрических величин.

Требуется знание следующих элементов и понятий:
Треугольник. Параллелограмм, прямоугольник, ромб, квадрат. Трапеция. Окружность и круг. Окружность, вписанная в треугольник, и окружность, описанная около треугольника. Многоугольник. Сумма углов выпуклого многоугольника. Величина угла, градусная мера угла, соответствие между величиной угла и длиной дуги окружности. Длина отрезка, ломаной, окружности; периметр многоугольника. Площадь треугольника, параллелограмма, трапеции, круга, сектора.

Пример 1

В тругольнике ABC угол C равен 90°, AB = 10, $B C = \sqrt{19}$ . Найдите cos A

Решение

$\cos A = \frac{A C}{A B}$
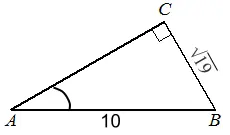
По теореме Пифагора: $A B^{2} = A C^{2} + C B^{2}$ , $A C^{2} = A B^{2} - C B^{2}$ , $A C = \sqrt{100 - 19} = \sqrt{81} = 9$
$\cos A = \frac{9}{10} = 0,9$
Ответ: 0,9

Пример 2

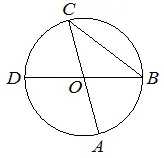
Отрезки AC и BD — диаметры окружности с центром O. Угол ACB равен 32°. Найдите угол AOD. Ответ дайте в градусах.

Решение

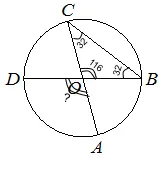
Раcсмотрим треугольник OCB:
Стороны треугольника OC и OB являются радиусами , а значит они равны. Таким образом, треугольник OCB является равнобедренным.
Из свойств равнобедренного треугольника известно, что углы при основании равны, значит угол OBC так же равен 32°, как и угол OCB
Зная два угла треугольника можно найти третий угол. Сумма трёх углов любого треугольника равна 180°, значит:
$∠ C O B = 180 - 32 - 32 = 116 °$
Найденный угол OBC и искомый угол AOD являются вертикальными, а значит они равны.
$∠ A O D = ∠ D O A = 116 °$
Ответ: 116